クイックソートのアルゴリズムをわかりやすく解説します！

2022 2/06

2022年2月6日

こんにちは！
今井(@ima_maru)です。

今回は、ソーティングルゴリズムの一つ「クイックソート」について、触れていきます。

できるだけ簡単にわかりやすく解説していきたいと思います！

この記事に書かれていること

クイックソートとは？
ソートって何？
分割統治法って何？
クイックソートの実際の処理とC言語/C++のコード

C言語/C++のソースコードは一番下にありますので必要な方はスクロールお願いします。

それでは解説に移ります！

クイックソート（Quick sort）とは？

クイックソートとは、C. A. R. Hoareさんが考案した「ソーティングアルゴリズム」の一種で、内部ソートの中では最も速いといわれているアルゴリズムです。

とりあえず、一番速いソート方法って覚えてください！

もちろん、それ以外にも同じぐらい速いソーティング方法はあり、条件や最悪の場合などを考えればクイックソートより速くなることあります。

この記事の終わりに、ほかの高速なソーティングアルゴリズムの紹介やクイックソートとの比較などを書きますので是非ご覧ください。

ソートが何かわからない方へ

ソートとは、本をタイトル順に並べることだったり、生徒を身長順に並べることだったり、順序のつけられるものを順序通りに並べなおす行為のことです。

例えば、優先度をつけてそれ通りにタスクを実行したいとき、ありますよね。

以下のようなタスクがこのように並んでいたらどうでしょうか？

（優先度70）一週間後のテストの勉強をする。
（優先度50）二週間後までの課題を終わらせる。
（優先度20）旅行の計画を立てる。

この順に並んでいるならば上から処理していけば大丈夫ですね。

しかし、「課題が二週間後までではなく、今日までだった！」と気づいたらどうでしょう。

（優先度70）一週間後のテストの勉強をする。
（優先度99）「今日の24:00締め切り」の課題を終わらせる。
（優先度20）旅行の計画を立てる。

優先度が99に上がり、優先度順ではなくなってしまいました。

ここでソートが必要になります。

（優先度99）「今日の24:00締め切り」の課題を終わらせる。
（優先度70）一週間後のテストの勉強をする。
（優先度20）旅行の計画を立てる。

こんな風にソートを行い、上から優先度順に並ぶように整列します。

プログラミングしていく上で、データが数字順に並んでいたほうがいいことはたくさんあります。

そんな時、このソート、すなわち、順番どおりに並べるということが必要になります。

今回の例に挙げたような3個ぐらいのデータでは何も問題ないですが、1万、10万というデータ数を扱うことを考えるとどうでしょうか？

効率よくソートする方法を知らなければ、とっても遅いプログラムになってしまいます。

そこで登場するのが効率の良いソートの一つが、今回の主役「クイックソート」なんです。

それでは、クイックソートのアルゴリズム解説に移りましょう！

クイックソートの主な考え方をわかりやすく解説！

クイックソートは分割統治法の一種

クイックソートは分割統治法というアルゴリズムの一種です。

分割統治法とは、そのままでは解くことの難しい大きな問題を、小さな問題に分割して考えるという手法です。

分割統治法とは、大きな問題を小さな問題の集合ととらえて、その小さな問題をすべて解くことで元の大きな問題の答えを得ようとする手法です。

トランプを買った時の順番に並べなおすとき、皆さんならどうしますか？

私だったら以下のようにします。

トランプを順番通りに並べなおす

52枚のカードをマーク別に分ける
- 13枚 ♠スペード
- 13枚 ♥ハート
- 13枚 ♣クローバー
- 13枚 ♦ダイヤ
それぞれのマークについて13枚（A~K）を並び替えて最後に合わせる

皆さんもこうするのではないでしょうか？

どうして、その４つのマーク別に分類するのか？

これは、単純な理由で「枚数が少ないほうが並べなおしやすいから」です。

このように52枚のカードをそのまま並び替えるのではなく、「一度4つのマーク別に分割してから、それぞれを並び替えて最後にくっつける」という手法をとるのが分割統治法の考え方です。

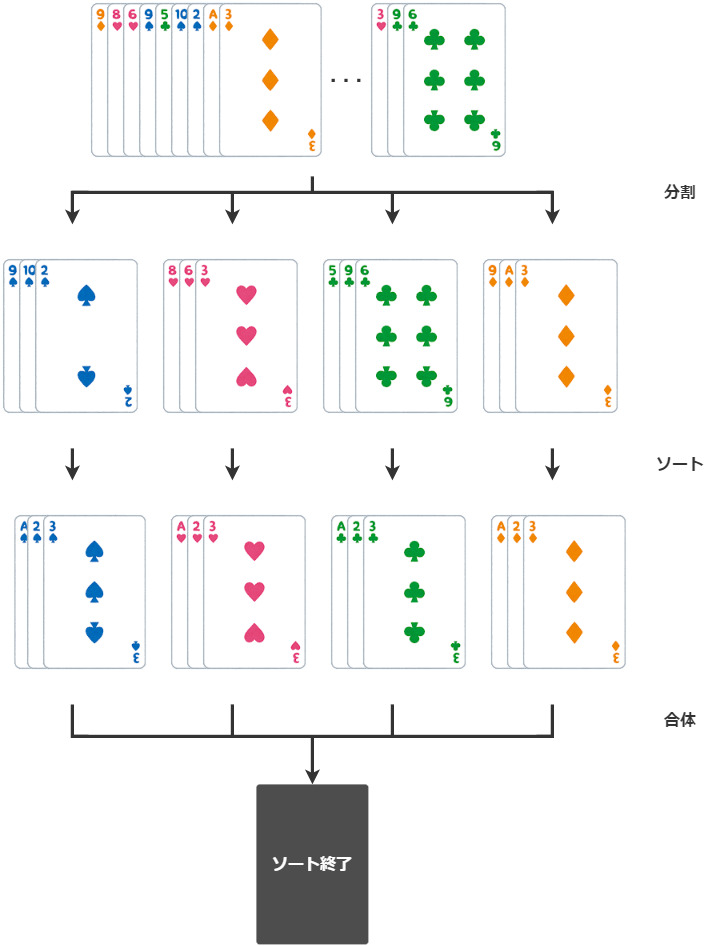
今回のクイックソートは、基準値をとることで元のデータを分割していきます。

クイックソートは実際何を行っているのか？

ここではクイックソートの実際の処理ではなく主な考え方について書きます。
（実際の処理は下で解説）

先ほども書きました通り、クイックソートは、元のデータを分割していく分割統治法という手法を用います。

クイックソートは、データを分割する際に、基準より大きい値と小さい値という条件で2分割します。

実はこの「基準より大きい値と小さい値」という条件がクイックソートの「核」となる部分です。

説明のために0~19までの数字をランダムに並べ替えたものを用意します。

↓ 0～19までの数字20個（ランダム） ↓

この数字たちを、0から順に0, 1, 2, 3... 19とソートしたいと思います。

まずは、基準値（ピボット）を決める必要があります。

今回は左端の「10」を基準値としてみましょう。

基準値を決めたら、基準値より小さい値と基準値より大きい値で場合分けしていきます。

左に小さい値、右に大きい値を置いていきましょう。

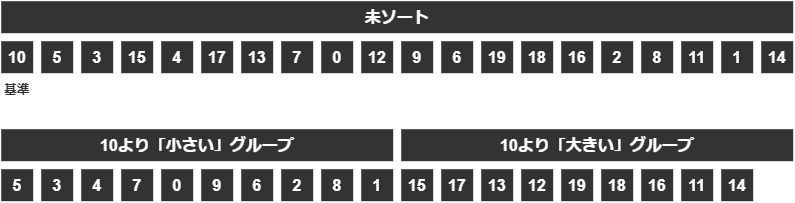
そうしたら、「0~9」は左のグループに入り、「11~19」は右のグループに入ります。

基準となった「10」は右のグループに入れておきましょう。

ここまでの結果、新しい2つのグループ「x<10のグループ」「10≦xのグループ」に分割できました。

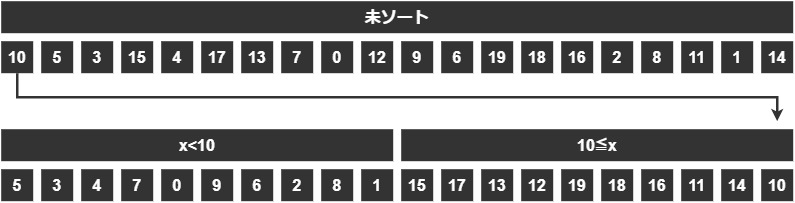
当たり前ですが、左のグループと右のグループの関係性を考えてみると、

「左のグループのどの値も、右のグループのどの値よりも小さい」

ということがわかると思います。

例えば、1(左)と19(右)を比べても、9(左)と10(右)を比べても、絶対に右のグループのデータのほうが大きい値なんです。

言ってることは単純で、「基準の値より小さい値と大きい値」に分けているから、右のグループのほうが絶対に大きいねってことです。

このことがわかると、左のグループと右のグループをそれぞれソートしてくっつければ順番どおりになることがわかるのです。

先ほどのトランプの例と同じです。

今の分割を先ほどの左のグループについてもう一回行いましょう。

一連の分割方法

基準値を決める
基準値より小さいグループと大きいグループに分ける
基準値を大きいグループのほうに入れる

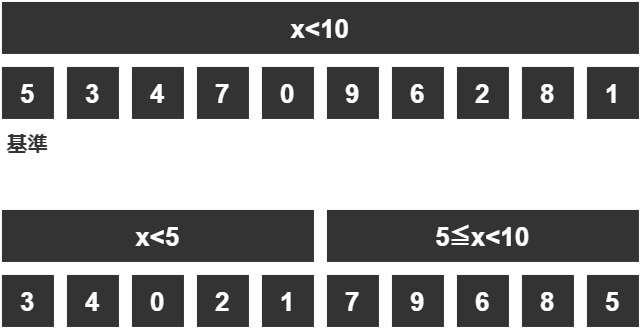
ここでも「左のグループの値 < 右のグループの値」という関係が成り立っていることに注意しましょう。

さらにこのグループとは別に、10以上のグループにもこの操作を行いましょう。

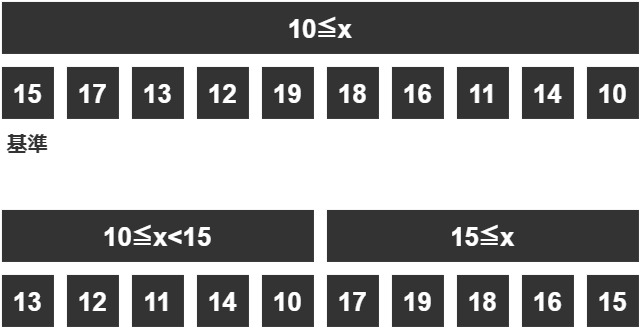
これも同じです。

そうすると、どうやらまた新しい2グループに分割できることがわかります。

これが、分割統治法の考え方「小さな問題に分割して考える」ということです。

今までの流れをまとめて、クイックソートの流れ図を書いてみましょう。

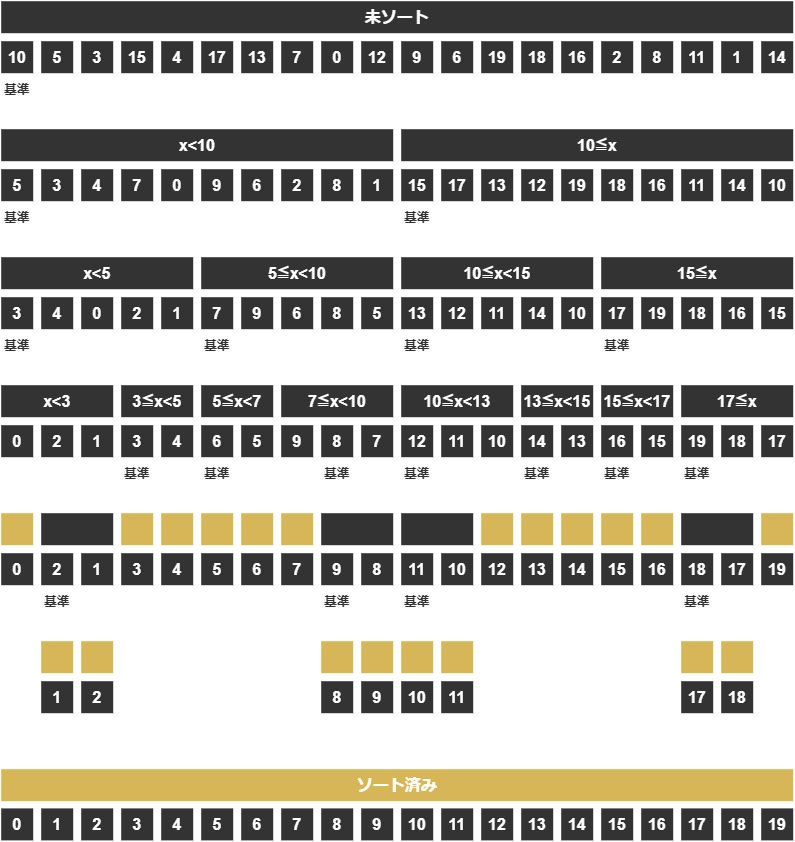
このように基準値をもとに分割するというのが、クイックソートの主な流れです。

以上より、クイックソートとは、

「基準値（ピボット）と比較して小さい値と大きい値に分ける」という処理を、分割されたグループそれぞれについて繰り返し行っていく

というソーティングアルゴリズムということもできます。

そうすると最終的にすべてのグループのデータ数が1個になり、それらを合わせればソート済みのデータとなるのです。

最終的に、データ数が2つや3つになりますが、その際の処理は少しイメージしにくいかもしれません。実際にコードを見てみるとどういう処理がされるのかわかるかもしれません。

クイックソートのアルゴリズム、どのように実現するか？

実際の処理方法は動画で理解した後、それと照らし合わせながらソースコードを見るのが効率的だと思います。

わかりやすい動画を張っておきますので参考にしてみてください。

クイックソートのわかりやすい解説動画

真ん中の値を基準値に取っている
基準値の取り方次第で効率が良くない場合がある

降順（大きい値から小さい値）になるようにソート
中規模のソート（4:25～）
バブルソート、シェーカーソートとの比較（5:03～）

C言語/C++で書くクイックソート

初めに言っておきますが、こんな長いクイックソートのコードを書くより、内容的にも労力的にも、用意されているライブラリの関数を使うのがいいです。

あくまで、アルゴリズムの勉強ということにお使いくださいませ。

C++をベースに書いています。たぶんCでも動きます。

#include <stdio.h>

//値を交換する関数
void swap(int *a, int *b) {
	int temp = *a;
	*a = *b;
	*b = temp;
}

/*クイックソート*/
void QuickSort(int A[], int left, int right)
{
	// 変数定義
	int Left, Right;
	int pivot;

	// 初期値は引数から
	Left = left; Right = right;

	// 基準は真ん中に設定
	pivot = A[(left + right) / 2];

	// ソーティング
	while (1) {

		// 基準より小さい値を左から見つけていく
		while (A[Left] < pivot) Left++;

		// 基準より大きい値を右から見つけていく
		while (pivot < A[Right]) Right--; 

		// 見つかった値の順序が逆になったら終了 
		if (Left >= Right) break;

		// 値を交換
		swap(&A[Left], &A[Right]);

		// 次の値に移動
		Left++; Right--;

	}

	//左のデータ群を対象としてクイックソートを再帰
	if (left < Left - 1) QuickSort(A, left, Left - 1);

	//右のデータ群を対象としてクイックソートを再帰
	if (Right + 1 < right) QuickSort(A, Right + 1, right);

}

クイックソートはなぜ高速なのか？どのくらい速いのか？

実際どのくらい速いのか？ほかのソートアルゴリズムと比較する。

クイックソートはほかの多くのソーティングアルゴリズムよりも高速に動作します。

その中でも「クイックソート」「マージソート」「ヒープソート」は非常に速いソートアルゴリズムです。

計算量は\(O\)（オーダ）と呼ばれる記号によってよく表され、 \(O(n^2)\)の場合はデータ数\(n\)に対して\(n^2\)に比例した計算量が必要という意味になります。

ソートアルゴリズム	平均計算量	最悪計算量
クイックソート	\(O(nlogn)\)	\(O(n^2)\)
マージソート	\(O(nlogn)\)	\(O(nlogn)\)
ヒープソート	\(O(nlogn)\)	\(O(nlogn)\)
挿入ソート	\(O(n^2)\)	\(O(n^2)\)
選択ソート	\(O(n^2)\)	\(O(n^2)\)
バブルソート	\(O(n^2)\)	\(O(n^2)\)

ソートアルゴリズムの種類と計算量

基本的に処理数はデータ数に応じて爆発的に増えていきますが、その増え方が\(O(nlogn)\)と\(O(n^2)\)で全く違います。

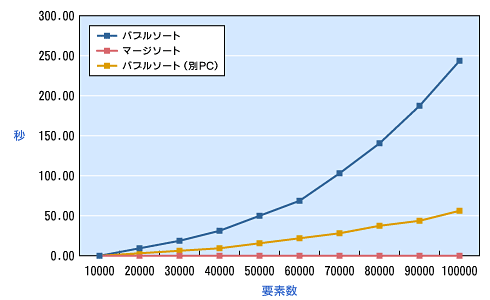
以下の図を見てください。

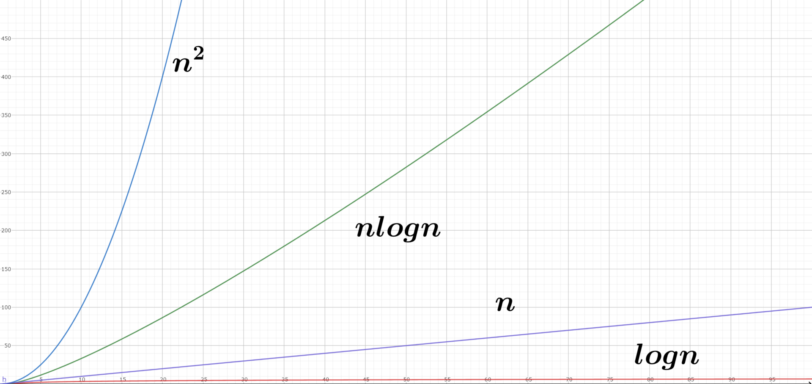
このグラフから掴んでいただきたいのは、\(O(nlogn)\)と\(O(n^2)\)では「次元が違う」レベルで速度が違うということです。

実際どのくらいの処理時間になるのか気になる方は、以下の記事を参考にしてみてください。（プログラミング言語やPCのスペックによっても大きく左右されるので注意してください。）

Qiita

Pythonで学ぶアルゴリズム　第22弾：並べ替え（ソート方法の比較） - Qiita #Pythonで学ぶアルゴリズム< ソート方法の比較 >##はじめに基本的なアルゴリズムをPythonで実装し，アルゴリズムの理解を深める．その第22弾として今まで学んできた...

＠IT

ソート処理時間、選ぶアルゴリズムでこんな差が！プログラミングの基礎となる考え方、アルゴリズムを理解しているだろうか？ ITエンジニアに贈る、アルゴリズム入門。

クイックソートが高速な理由は無駄がないから

「クイックソートはなぜ速いのでしょうか？」

それは、平均計算量が小さいからです。

当たり前ですが、処理数が少ないから速いんです。

コンピュータは比較や書き込みといった処理を1つ1つ実行していくわけですから、それらの処理数が少なければ少ないほど短い時間でプログラムが終了します。

「では、なぜ平均計算量が小さいのでしょうか？」

この答えは計算上小さいからと言ってしまえばそれまでなのですが、それだとつまらないので直感的に理解してみましょう。

イメージは、無駄な比較が少ないからです。

無駄な比較とは、例えばバブルソートや選択ソートなどに見られる同じ値同士の比較です。

この無駄な比較をなくすためには、なにか革新的な工夫が必要です。

クイックソートの場合は、基準値未満のグループと基準値以上のグループに分けて、それらを別々の小さい問題に分けて考えるという分割統治法の考えが革新的で、それによって無駄な比較を省けているといっても良いでしょう。

ほかの高速なソートアルゴリズムもなんらかの革新的な工夫がなされています。

例えばマージソートは2つのグループを合体する際にこれまで比較された値同士の比較がないようなマージという処理が革新的ですし、ヒープソートも最大値を取得する際のヒープ構造を活かしたダウンヒープという処理が革新的です。

こういった革新的な工夫で無駄な比較を省いているため、圧倒的に速い速度を誇るのです。

クイックソートも実は遅い場合がある。最良の場合と最悪の場合とは？

平均的に高速で動作するクイックソートにも実は非常に遅くなってしまう場合があります。

クイックソートは分割によってできる2つのグループのデータ数が均等に近いほど高速に動作し、逆に偏ったデータ数になるほど遅くなります。

つまり、1000個⇒500個が2つ⇒250個が4つ⇒125個が8つ⇒...と分割される場合が最良で、1000個⇒1個と999個⇒1個と1個と998個⇒1個と1個と1個と997個⇒...というように分割される場合が最悪です。

言い換えれば以下のようになります。

最良の場合：すべての分割において、基準値（pivot）に選ばれた値がその配列の中の中央値となる場合。
- 基準値が中央値＝基準値より小さい値と大きい値の個数がほぼ均等
- 分割後の2つのグループのデータ数がほぼ均等
最悪の場合：すべての分割において、基準値（pivot）に選ばれた値がその配列の中の最小値か最大値となる場合。
- 基準値とそれら以外の値全てという偏った分割が行われる

例えば、100万個のデータに対してのクイックソートを考えてみましょう。

ここで1回の分割にかかる処理は（基準値も含む）グループ内のすべてのデータそれぞれと基準値を比較する処理ですからデータ数回かかるものだと思ってください。

最良の場合は毎回ほぼ2等分に分割できる場合で、この場合20分割でデータ数が1になりますので、単純計算だと100万回+50万回×2グループ+25万回×4グループ+...2回×50万グループ＝2000万回ほどになります。

最良の場合はデータ数が100万⇒99万9999⇒99万9998⇒...と減っていくわけですから、100万回+99万9999回+99万9998回+...+2≒5000億回ほどになります。

最良の場合は2000万回なのに対して最悪の場合は5000億回なので、明らかに処理数が違うことが分かりますね。

実際この最悪の場合に近い場合のクイックソートは、バブルソート同様の速度を叩き出すことになります。

Sideswipe

Quicksort の攻撃方法 - Sideswipe 以前 Quicksort の計算量について話したので、ブログにも書いておきます。 QuickSort Killer from Kazuya Gokita 参考にしたのは、 M. D. MCILROY の A Killer Adversary f...

Programming Place Plus

クイックソート | Programming Place Plus　アルゴリズムとデータ構造編【整列アルゴリズム】　第６章

クイックソート以外の高速なソーティングアルゴリズム！

最後に、ほかの高速なソーティングアルゴリズム、また、基本的なソーティングアルゴリズムの動画をご紹介して終わりにしたいと思います。

ソーティングアルゴリズムの比較動画

これはいろいろなソーティングアルゴリズムを紹介している動画です。

左上にソート名が書いてあります。

また、ソートするデータ数や速度設定が違うので注意してください。

4番目に紹介されているのがマージソート（Merge sort）、5番目に紹介されているヒープソート（Heap sort）です。

どちらも、とても高速なソーティングアルゴリズムとして有名です。

今後紹介していけたらと思います。

【もっと早く知っておけばよかった...。】情報系を学んでいる学生におすすめのサービス！

オンライン学習サービス	対象者	特徴
Progate	超初心者	プログラミング入門・基本無料
Udemy	初心者～中級者	豊富な動画教材・セールでお得・教材購入
侍エンジニアPlus	初心者～中級者	現役エンジニアに質問できる環境・月額制
Paiza	初心者	競プロ入門・就活/インターン・無料
ドットインストール	初心者	動画教材・成果物ができる・基本無料
Recursion	初心者	コンピュータサイエンス基礎・基本無料
AtCoder	中級者～上級者	競技プログラミング・アルゴリズム・無料
Kaggle	中級者～上級者	AI・データサイエンス・競プロ・英語・無料