メタヒューリスティクスとは？わかりやすく解説！

今回は、メタヒューリスティクスについて解説します。

メタヒューリスティクスとは、組み合わせ最適化問題における汎用的な問題解決手法のことで、いままでにいろんな手法が生まれています。

現実問題において、問題解決の手法としてメタヒューリスティクスが多く使われています。

メタヒューリスティクスとは？

組み合わせ最適化問題によく使われる「メタヒューリスティクス」とは一体何なのか？

見ていきましょう。

ヒューリスティクス（Heuristics）とは？

ヒューリスティクスとは、プログラミングや心理学の分野で使われることがある単語です。

単語自体の意味としては、「発見的な」「経験則」などが当てはまります。

問題解決や意思決定の場において、システマティックないしは数理的な手順（アルゴリズム）によらずにほどほどに満足できる近似的な解を得る解法。

引用元：メタヒューリスティクスとは何か

ヒューリスティクス（heuristic）または発見的（手法）とは、必ず正しい答えを導けるわけではないが、ある程度のレベルで正解に近い解を得ることができる方法である。発見的手法では、答えの精度が保証されない代わりに、回答に至るまでの時間が少ないという特徴がある。

引用元：wikipedia

このように説明されます。

かみ砕いていえば、「論理的ではなく『勘』に頼っておおよその答えを求める手法」です。

つまり、「厳密解を求める代わりに近似解を求める」という「近似解法」の一種ですね。

メタヒューリスティクスとは？

プログラミングで使われるのが多いのは、「メタヒューリスティクス」という単語です。

組合せ最適化問題のアルゴリズムにおいて、特定の計算問題に依存しないヒューリスティクスのことである。 近年では、上記の定義から拡張され、特定の問題に依存しない、汎用性の高いヒューリスティクス全般を指すこともある。

引用元：wikipedia

かみ砕いていえば、「あらゆる組み合わせ最適化問題に適用できる近似解法」です。

では組み合わせ最適化問題というものが何か見ていきましょう。

組み合わせ最適化問題とは？

組み合わせ最適化問題の例をいくつかあげましょう。

巡回セールスマン問題

これは、複数の都市をどのようにまわるのが良いかを求める問題です。

都市数が10の場合は、\(10!=3628800\)の全通りを探索すれば厳密解が求まるのですが、

都市数が20の場合は、\(20!=2432902008176600000\)通りを探索しなくてはなりません。

このように、都市数の増加によって、計算量が爆発的に増えてしまうという特徴があります。

一般的に、都市数が20を超えると現実的な計算時間で厳密解を求めることは不可能といわれています。

スケジューリング問題

スケジューリング問題とは、限られた資源に対してどのようにタスクを割り振っていくのが効率的かを求める問題です。

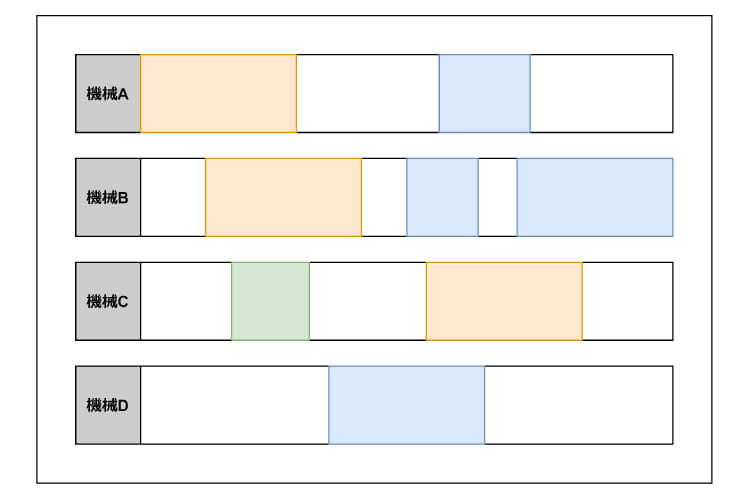
こちらの問題も、組み合わせが爆発的に増えるため、現実的な計算時間で厳密解を求めることは難しいといわれている問題です。

組み合わせ最適化問題とメタヒューリスティクス

このように、あらゆる組み合わせから最適解を求めようとする問題のことを、「組み合わせ最適化問題」と呼びます。

「組み合わせ最適化問題」は、現実問題として多く存在しています。

このような問題に対して、最適解/厳密解（すべての組み合わせの中で一番良い解）を必ず見つけだすようなことは、現実的に難しいことが多いです。

なので、メタヒューリスティクスでは、「比較的短い現実的な時間で、ある程度の精度で正解に近い解を見つけ出す」ということを目的とします。

メタヒューリスティクスの基本的な流れ

基本的なメタヒューリスティクスは、初期解から改善を繰り返すことで良い解を目指すということをしていきます。

巡回セールスマン問題を例に、以下のような巡回路を初期解として考えてみましょう。

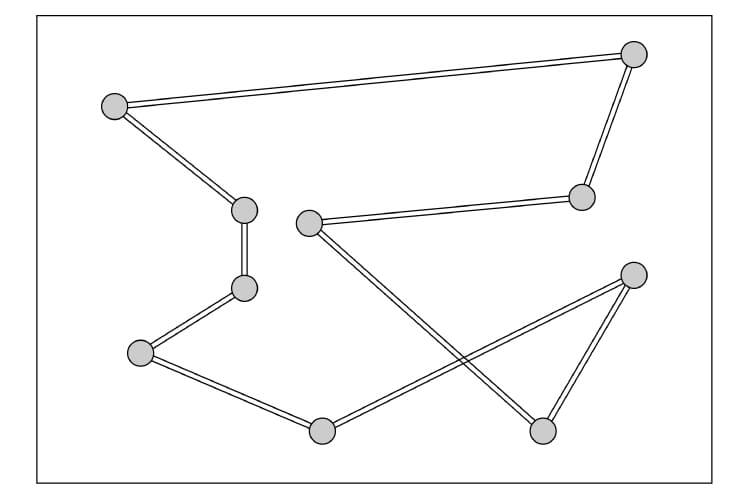
この解（巡回路）を基本として、「近傍」（きんぼう）というものを作ってみましょう。

「近傍」とは、基本となる解から、部分的に変更を加えて作られた解のことで、以下のような例が挙げられます。

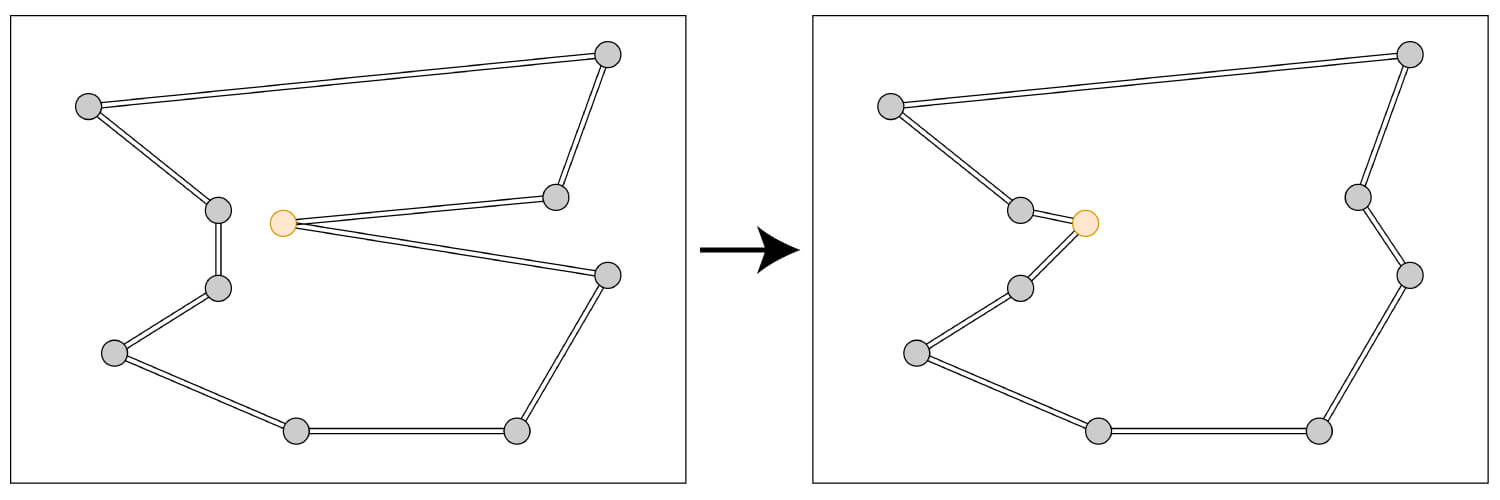
この近傍は、選んだ2辺をつなぎなおす「2-opt近傍」と呼ばれる近傍操作です。

黄色に色づけされた部分の巡回路の捻じれがなくなって、良い解になりましたね。

なので、次はこの近傍を基準として新しい近傍を作ってみましょう。

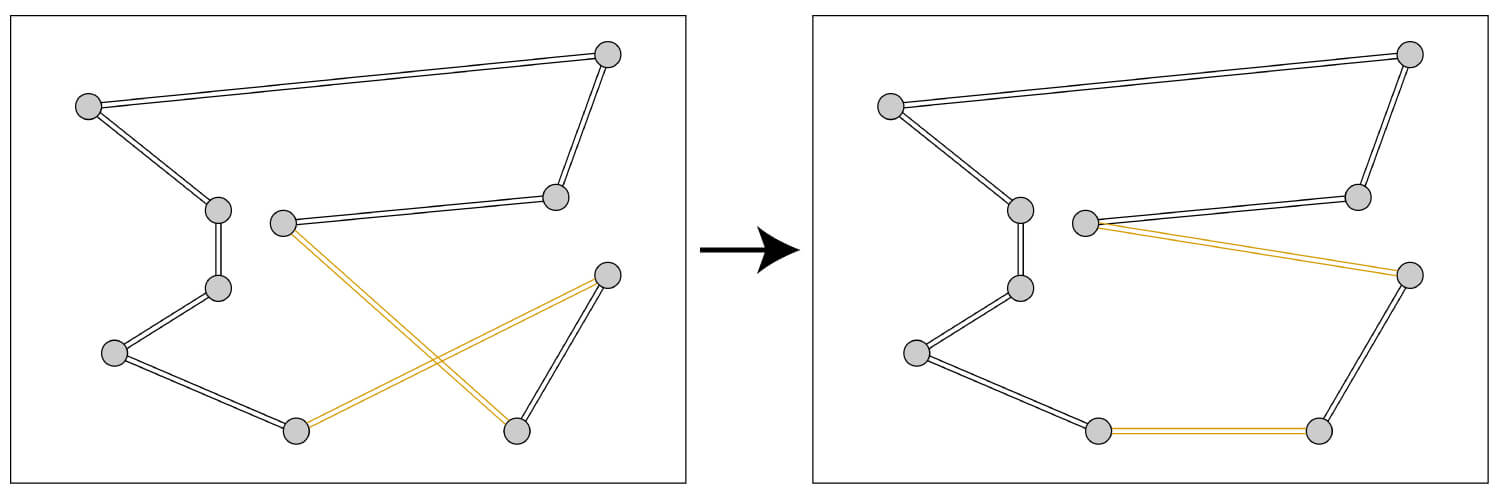
この近傍は、選んだ区間を異なる区間に挿入する「挿入近傍」と呼ばれる近傍操作です。

黄色に色付けされた都市が近い都市に結びつけられて、さらに良い解になりましたね。

いままでの流れを振り返ると、

というような流れでした。

言い換えれば、「部分的に改善を繰り返していくことで、良い解に近づいていく」ということですね。

実はこれは「局所探索法」「山登り法」と呼ばれるメタヒューリスティクスの基本的な手法で、大半のメタヒューリスティクスはこの考えにいろいろな工夫を入れた手法になります。

メタヒューリスティクスは「何か」からヒントを得ている

多くのメタヒューリスティクスは、生物の行動や繁殖、さらには金属加工などの様子からヒントを経ています。

例えば、先ほどの局所探索法の考えに、金属加工の「焼きなまし」のアイデアを取り入れた「焼きなまし法」。

生物の自然淘汰の考えを取り入れた「遺伝的アルゴリズム」。

蟻が餌を巣へと持ち帰る様子からヒントを経た「蟻コロニー最適化」。

このように、生物や物理現象などからヒントを得るということがあります。

メタヒューリスティクスが有効な問題の特徴

NP困難＝厳密な最適解を求めるのが難しい

メタヒューリスティクスを使う問題の特徴として、「NP困難」であるということが挙げられます。

「NP困難」とは、多項式時間で最適解を求めることができないということです。

要は、「現実的な時間で厳密解を求めることができそうにない」という意味です。

例えば、巡回セールスマン問題の都市数と処理数の関係は、

都市数	処理数
5	\(5!=120\)
10	\(10!=3628800\)
15	\(15!=1307674368000\)
20	\(20!=2432902008176600000\)

このようになります。

1処理の計算に0.1ミリ秒（10000分の1秒）しかかからなかったとしても、都市数20の場合、

\(243290200817660秒≒2815858806日≒7714682年\)

800万年近くかかってしまうという計算になります。

組み合わせ最適化問題では、全通りを試してみるというのが現実的に不可能ということが多いです。

そのため、「比較的短い現実的な時間で、ある程度の精度で正解に近い解を見つけ出す」というメタヒューリスティクスの手法が使われます。

1つの解を評価すること自体は容易

メタヒューリスティクスが適用できる問題の特徴として、「1回の解評価が容易」ということが挙げられます。

メタヒューリスティクスでは、一般的に、解の評価を何回も行います。

これは、解を何回も生成し、評価し、解の精度を高めていくからです。

そのため、一度の評価に時間がかかっていてはいけません。

比較的短時間で評価ができる評価関数を用いて、試行回数を稼ぎ、解の精度を高めていきます。

近接最適性（POP）が成り立つ

メタヒューリスティクスが適用できる問題の特徴として、「近接最適性」が成り立つということが挙げられます。

近接最適性とは、「良い解同士は何らかの類似構造を持つ」という概念のことです。

簡単に言えば、「良い解同士は似ている部分をたくさん持つ」ということです。

この性質がなければ、メタヒューリスティクスをうまく活かすことができません。

というのも、良い解と特徴が似ている解が評価された時に、似た評価値が出なければ部分的な改善がうまくいかないからです。

逆に、近接最適性が成り立たない例として、ぷよぷよが挙げられます。

ぷよぷよは、評価値に連鎖数が大きくかかわってきますが、一つでも違うマスにぷよを置いてしまうと、連鎖数ががらりとかわってしまうということがあります。

つまり、どこか一つでも間違った置き方をしてしまうと連鎖が途中で止まってしまうということがあるので、近接最適性は成り立ちません。

ゆえに、一般的なメタヒューリスティクスを適応するのは難しいと考えられます。

メタヒューリスティクスの種類

メタヒューリスティクスの枠組みを手法は色々ありますが、その中でも有名なものをいくつか紹介します。

山登り法（Local Search）

山登り法は、純粋な局所探索法のことで、メタヒューリスティクスの基本的な概念になっています。

※今後追加予定

焼きなまし法=アニーリング法（Simulated Annealing）

焼きなまし法（SA）は、山登り法が改善解にしか遷移しないのと違い、改悪解にも確率的に遷移するという特徴を持った近傍探索のメタヒューリスティクスです。

その際に、金属の焼きなましからヒントを得た「温度」というパラメータを使い、確率を変化させていきます。

※今後追加予定

遺伝的アルゴリズム（Genetic Algorithm）

遺伝的アルゴリズム（GA）は、生物の自然淘汰をモデルに作られたメタヒューリスティクスです。

蟻コロニー最適化（Ant Colony Optimization）

蟻コロニー最適化（ACO）は、蟻が餌を巣へと持ち帰る様子からヒントを得た、群知能のメタヒューリスティクスです。

※今後追加予定

以上「メタヒューリスティクスとは？わかりやすく解説！」でした！